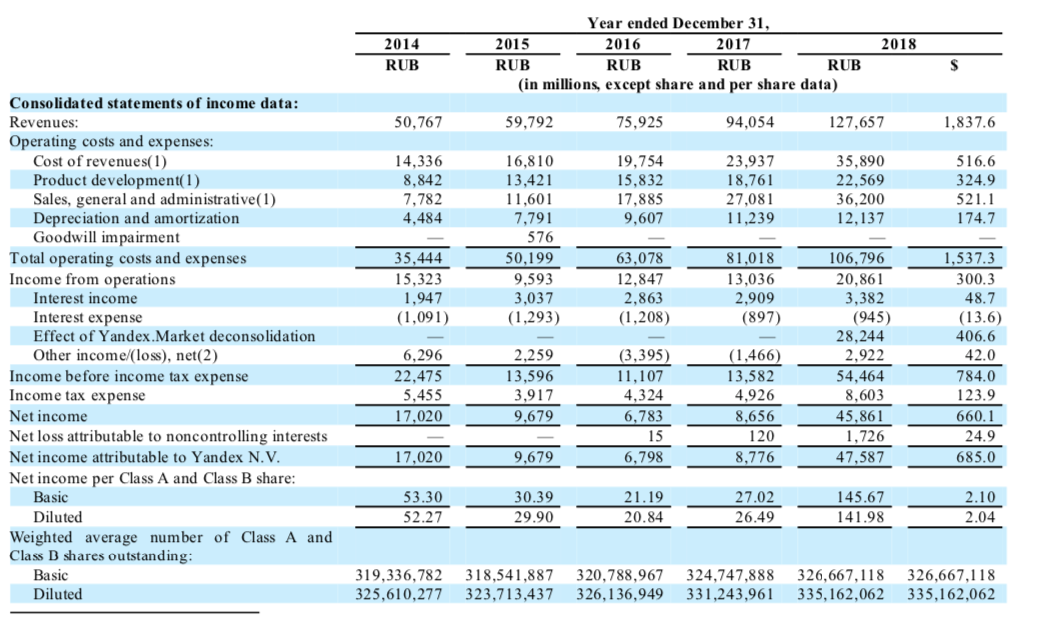
FWER=1−(1−α)m (family-wise error rate)
график для α=0.05
Поправка Бонферрони
αcorr=α/m
для двух тестов m=2 и уровне значимости в 5% αcorr=0.025:
FWER=1−(1−αcorr)m = 1−(1−0.025)2=0.05
Метод Шидака
αcorr=1−(1−α
)1/m
)1/m
Метод Холма
метод Холма — итерационный. То есть рассчитывается не единый уровень αα для всех тестов, а новый для каждого из тестов. Формула расчёта уровней коррекции выглядит такimport pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# подготавливаем данные
report = pd.DataFrame()
report['m'] = pd.Series([2, 3, 4, 5, 6, 7, 8, 9, 10]) # число тестов
report['alpha'] = 0.05 # исходный уровень значимости
# считаем поправки
report['Метод Бонферрони'] = report['alpha'] / report['m']
report['Метод Шидака'] = 1 - (1 - report['alpha']) ** (1 / report['m'])
# рассчитываем поправку Холма
def holm_correction(row):
m, alpha = int(row['m']), row['alpha'] # число тестов и уровень значимости
result = []
for i in range(m): # получаем номер текущего теста и считаем коррекцию
result += [alpha / (m - i)]
return result
# поскольку поправка Холма возвращает много результатов - возьмём среднее по ним
report['Поправки Холма'] = report.apply(holm_correction, axis=1)
report['Средний ур. знач. при поправке Холма'] = report['Поправки Холма'].apply(np.mean) # считаем средний уровень значимости с учётом поправки Холма
print(report)
# строим график
report.set_index('m')[['Метод Бонферрони', 'Метод Шидака', 'Средний ур. знач. при поправке Холма']].plot(grid=True)
# подписываем оси
plt.xlabel('Число тестов'), plt.ylabel('Уровень значимости')
plt.legend(title = 'Метод коррекции'), plt.title('Скорректированные уровни значимости')
plt.show()
На практике чаще всего применяют коррекцию Бонферрони — из-за простоты, но можно применять и коррекцию Холма, поскольку она более «щадящая» по отношению к мощности теста.
На практике это означает, что с таким низким уровнем значимости мы практически всегда будем оказываться в ситуации, когда нулевая гипотеза не отвергается и, возможно, будем совершать частые ошибки второго рода (то есть пострадает мощность теста). Это может произойти даже при коррекции для десяти сравнений и выше.
Чтобы справиться с этой проблемой, придумали специальные тесты для множественного сравнения гипотез:
- ANOVA — аналог t-теста для ситуаций сравнения трёх и более выборок;
- χ2-тест (читается «хи-квадрат») на независимость для сравнения пропорций, долей и шагов воронок — аналог z-теста для пропорций. Обратите внимание, что существует целое семейство тестов χ2, использующихся для самых разных целей. Для сравнения пропорций используется только тест на независимость (test of independence/association);
- Тест Краскела-Уоллиса — аналог теста Манна-Уитни для ситуации множественных сравнений. С тестом Манна-Уитни вы познакомитесь в следующей теме.